The global strong solutions of the 3D incompressible Hall-MHD system with variable density
Abstract
In this paper, we focus on the well-posedness problem of the three-dimensional incompressible viscous and resistive Hall-magnetohydrodynamics system (Hall-MHD) with variable density. We mainly prove the existence and uniqueness issues of the density-dependent incompressible Hall-magnetohydrodynamic system in critical spaces on 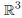
Keyword : variable density, Hall-MHD, global solution, critical spaces
How to Cite
An, S., Chen, J., & Han, B. (2024). The global strong solutions of the 3D incompressible Hall-MHD system with variable density. Mathematical Modelling and Analysis, 29(2), 288–308. https://doi.org/10.3846/mma.2024.17776

This work is licensed under a Creative Commons Attribution 4.0 International License.
References
H. Alfvén. Existence of electromagnetic-hydrodynamic waves. Nature, 150:405– 406, 1942. https://doi.org/10.1038/150405d0
M. Arichetogaray, P. Degond, A. Frouvelle and J.G. Liu. Kinetic formulation and global existence for the Hall-Magneto-hydrodynamics system. Kinetic and Related Models, 4(4):901–918, 2011. https://doi.org/10.3934/krm.2011.4.901
H. Bahouri, J.Y. Chemin and R. Danchin. Fourier analysis and nonlinear partial differential equations. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences]. 343, Springer, Heidelberg, 2011.
L.C. Campos. On hydromagnetic waves in atmospheres with application to the Sun. Ann. I. H. Poincaré, 10:37–70, 1998. https://doi.org/10.1007/s001620050050
D. Chae, P. Degond and J.G. Liu. Well-posedness for Hallmagnetohydrodynamics. Ann. I. H. Poincaré, 31(3):555–565, 2014. https://doi.org/10.1016/j.anihpc.2013.04.006
D. Chae and M. Schonbek. On the temporal decay for the Hallmagnetohydrodynamic equations. J. Differential Equations, 255(11):3971–3982, 2013. https://doi.org/10.1016/j.jde.2013.07.059
D. Chae and J. Wolf. On partial regularity for the steady Hallmagnetohydrodynamics system. Comm. Math. Phys., 339:1147–1166, 2015. https://doi.org/10.1007/s00220-015-2429-2
D. Chae and J. Wolf. On partial regularity for the 3D nonstationary Hall magnetohydrodynamics equations on the plane. SIAM J. Math. Anal., 48:443–469, 2016. https://doi.org/10.1137/15M1012037
R. Danchin. Density-dependent incompressible viscous fluids in critical spaces. Proceedings of the Royal Society of Edinburgh: Section A Mathematics, 133(6):1311–1334, 2003. https://doi.org/10.1017/S030821050000295X
R. Danchin. Well-posedness in critical spaces for barotropic viscous fluids with truly not constant density. Commun. Partial Differ. Equ., 32(9):1373–1397, 2007. https://doi.org/10.1080/03605300600910399
R. Danchin and J. Tan. The global solvability of the Hall-magnetohydrodynamics system in critical Sobolev spaces. arXiv.1912.09194, pp. 1–25, 2019.
R. Danchin and J. Tan. On the well-posedness of the Hallmagnetohydrodynamics system in critical spaces. Comm. Partial Differential Equations, 46(1):31–65, 2021. https://doi.org/10.1080/03605302.2020.1822392
N. Duan. Global well-posedness and analyticity of solutions to threedimensional Hall-MHD equations. J. Math. Anal. Appl., 463(2):506–516, 2018. https://doi.org/10.1016/j.jmaa.2018.03.020
E. Dumas and F. Sueur. On the weak solutions to the Maxwell–Landau–Lifshitz equations and to the Hall-magneto-hydrodynamic equations. Comm. Math. Phys., 330:1179–1225, 2014. https://doi.org/10.1007/s00220-014-1924-1
J. Fan, A. Alsaedi, Y. Fukumoto, T. Hayat and Y. Zhou. A regularity criterion for the density-dependent Hall-magnetohydrodynamics. Z. Anal. Anwend., 34(3):277–284, 2015. https://doi.org/10.4171/ZAA/1539
J. Fan, S. Huang and G. Nakamura. Well-posedness for the axisymmetric incompressible viscous Hall-magnetohydrodynamic equations. Computers and Mathematics with Applications, 74:2438–2443, 2017.
J. Fan, X. Jia, G. Nakamura and Y. Zhou. On well-posedness and blowup criteria for the magnetohydrodynamics with the Hall and ion-slip effects. Z. Angew. Math. Phys., 66:1695–1706, 2015. https://doi.org/10.1007/s00033-015-0499-9
D. Fang, B. Han and T. Zhang. Global existence in critical spaces for density dependent incompressible viscoelastic fluids. Acta Appl. Math., 130:51–80, 2014. https://doi.org/10.1007/s10440-013-9838-z
T. Forbes. Magnetic reconnection in solar flares. Geophysical Astrophysical Fluid Dynamics, 34:277–284, 1991.
F. He, B. Ahmad, T. Hayat and Y. Zhou. On regularity criteria for the 3D Hall-MHD equations in terms of the velocity. Nonlinear Anal. Real World Appl., 32:35–51, 2016. https://doi.org/10.1016/j.nonrwa.2016.03.014
J.D. Huba. A tutorial on Hall magnetohydrodynamics. Lecture Notes in Physics, 615:166–192, 2008. https://doi.org/10.1007/3-540-36530-3_9
J.D. Huba and L.I. Rudakov. Hall magnetohydrodynamics of neutral layers. Physics of Plasmas, 10(8):3139–3150, 2003. https://doi.org/10.1063/1.1582474
G. Nakamura J. Fan, Y. Fukumoto and Y. Zhou. Regularity criteria for the incompressible Hall-MHD system. Z. Angew. Math. Mech., 95(11):1156–1160, 2015. https://doi.org/10.1002/zamm.201400102
Z. Lei and F. Lin. Global mild solutions of Navier–Stokes equations. Comm. Pure Appl. Math., 64(9):1297–1304, 2011. https://doi.org/10.1002/cpa.20361
M. Lighthill. Studies on magneto-hydrodynamic waves and other anisotropic wave motions. Philos. Trans. R. Soc. Lond. Ser. A, 252(1014):397–430, 1960. https://doi.org/10.1098/rsta.1960.0010
P.D. Mininni, D.O. Gomez and S.M. Mahajan. Dynamo action in magnetohydrodynamics and Hall-magnetohydrodynamics. The Astrophysical Journal, 567:81–83, 2003. https://doi.org/10.1086/339850
D.A. Shalybkov and V.A. Urpin. The Hall effect and the decay of magnetic fields. Astronomy & Astrophysics, 321(2):685–690, 1997.
R. Wan and Y. Zhou. On global existence, energy decay and blow-up criteria for the Hall-MHD system. Journal of Differential Equations, 259(11):5982–6008, 2015. https://doi.org/10.1016/j.jde.2015.07.013
R. Wan and Y. Zhou. Global well-posedness, BKM blow-up criteria and zero h limit for the 3D incompressible Hall-MHD equations. Journal of Differential Equations, 267(6):3724–3747, 2019. https://doi.org/10.1016/j.jde.2019.04.020
R. Wan and Y. Zhou. Global well-posedness for the 3D incompressible Hall-magnetohydrodynamic equations with Fujita-Kato type initial data. Journal of Mathematical Fluid Mechanics, 21(5):1–18, 2019. https://doi.org/10.1007/s00021-019-0410-0
M. Wardle. Star formation and the Hall effect. Astrophysics & Space Science, 292:317–323, 2004. https://doi.org/10.1023/B:ASTR.0000045033.80068.1f
S. Weng. On analyticity and temporal decay rates of solutions to the viscous resistive Hall-MHD system. Journal of Differential Equations, 260(8):6504–6524, 2016. https://doi.org/10.1016/j.jde.2016.01.003
X. Wu, Y. Yu and Y. Tang. Well-posedness for the incompressible Hall-MHD equations in low regularity spaces. Mediterranean Journal of Mathematics, 15(2):1–14, 2018. https://doi.org/10.1007/s00009-018-1096-x
X. Zhao. Decay of solutions to a new Hall-MHD system in R3. C. R. Math. Acad. Sci. Paris, 355(3):310–317, 2017. https://doi.org/10.1016/j.crma.2017.01.019
M. Arichetogaray, P. Degond, A. Frouvelle and J.G. Liu. Kinetic formulation and global existence for the Hall-Magneto-hydrodynamics system. Kinetic and Related Models, 4(4):901–918, 2011. https://doi.org/10.3934/krm.2011.4.901
H. Bahouri, J.Y. Chemin and R. Danchin. Fourier analysis and nonlinear partial differential equations. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences]. 343, Springer, Heidelberg, 2011.
L.C. Campos. On hydromagnetic waves in atmospheres with application to the Sun. Ann. I. H. Poincaré, 10:37–70, 1998. https://doi.org/10.1007/s001620050050
D. Chae, P. Degond and J.G. Liu. Well-posedness for Hallmagnetohydrodynamics. Ann. I. H. Poincaré, 31(3):555–565, 2014. https://doi.org/10.1016/j.anihpc.2013.04.006
D. Chae and M. Schonbek. On the temporal decay for the Hallmagnetohydrodynamic equations. J. Differential Equations, 255(11):3971–3982, 2013. https://doi.org/10.1016/j.jde.2013.07.059
D. Chae and J. Wolf. On partial regularity for the steady Hallmagnetohydrodynamics system. Comm. Math. Phys., 339:1147–1166, 2015. https://doi.org/10.1007/s00220-015-2429-2
D. Chae and J. Wolf. On partial regularity for the 3D nonstationary Hall magnetohydrodynamics equations on the plane. SIAM J. Math. Anal., 48:443–469, 2016. https://doi.org/10.1137/15M1012037
R. Danchin. Density-dependent incompressible viscous fluids in critical spaces. Proceedings of the Royal Society of Edinburgh: Section A Mathematics, 133(6):1311–1334, 2003. https://doi.org/10.1017/S030821050000295X
R. Danchin. Well-posedness in critical spaces for barotropic viscous fluids with truly not constant density. Commun. Partial Differ. Equ., 32(9):1373–1397, 2007. https://doi.org/10.1080/03605300600910399
R. Danchin and J. Tan. The global solvability of the Hall-magnetohydrodynamics system in critical Sobolev spaces. arXiv.1912.09194, pp. 1–25, 2019.
R. Danchin and J. Tan. On the well-posedness of the Hallmagnetohydrodynamics system in critical spaces. Comm. Partial Differential Equations, 46(1):31–65, 2021. https://doi.org/10.1080/03605302.2020.1822392
N. Duan. Global well-posedness and analyticity of solutions to threedimensional Hall-MHD equations. J. Math. Anal. Appl., 463(2):506–516, 2018. https://doi.org/10.1016/j.jmaa.2018.03.020
E. Dumas and F. Sueur. On the weak solutions to the Maxwell–Landau–Lifshitz equations and to the Hall-magneto-hydrodynamic equations. Comm. Math. Phys., 330:1179–1225, 2014. https://doi.org/10.1007/s00220-014-1924-1
J. Fan, A. Alsaedi, Y. Fukumoto, T. Hayat and Y. Zhou. A regularity criterion for the density-dependent Hall-magnetohydrodynamics. Z. Anal. Anwend., 34(3):277–284, 2015. https://doi.org/10.4171/ZAA/1539
J. Fan, S. Huang and G. Nakamura. Well-posedness for the axisymmetric incompressible viscous Hall-magnetohydrodynamic equations. Computers and Mathematics with Applications, 74:2438–2443, 2017.
J. Fan, X. Jia, G. Nakamura and Y. Zhou. On well-posedness and blowup criteria for the magnetohydrodynamics with the Hall and ion-slip effects. Z. Angew. Math. Phys., 66:1695–1706, 2015. https://doi.org/10.1007/s00033-015-0499-9
D. Fang, B. Han and T. Zhang. Global existence in critical spaces for density dependent incompressible viscoelastic fluids. Acta Appl. Math., 130:51–80, 2014. https://doi.org/10.1007/s10440-013-9838-z
T. Forbes. Magnetic reconnection in solar flares. Geophysical Astrophysical Fluid Dynamics, 34:277–284, 1991.
F. He, B. Ahmad, T. Hayat and Y. Zhou. On regularity criteria for the 3D Hall-MHD equations in terms of the velocity. Nonlinear Anal. Real World Appl., 32:35–51, 2016. https://doi.org/10.1016/j.nonrwa.2016.03.014
J.D. Huba. A tutorial on Hall magnetohydrodynamics. Lecture Notes in Physics, 615:166–192, 2008. https://doi.org/10.1007/3-540-36530-3_9
J.D. Huba and L.I. Rudakov. Hall magnetohydrodynamics of neutral layers. Physics of Plasmas, 10(8):3139–3150, 2003. https://doi.org/10.1063/1.1582474
G. Nakamura J. Fan, Y. Fukumoto and Y. Zhou. Regularity criteria for the incompressible Hall-MHD system. Z. Angew. Math. Mech., 95(11):1156–1160, 2015. https://doi.org/10.1002/zamm.201400102
Z. Lei and F. Lin. Global mild solutions of Navier–Stokes equations. Comm. Pure Appl. Math., 64(9):1297–1304, 2011. https://doi.org/10.1002/cpa.20361
M. Lighthill. Studies on magneto-hydrodynamic waves and other anisotropic wave motions. Philos. Trans. R. Soc. Lond. Ser. A, 252(1014):397–430, 1960. https://doi.org/10.1098/rsta.1960.0010
P.D. Mininni, D.O. Gomez and S.M. Mahajan. Dynamo action in magnetohydrodynamics and Hall-magnetohydrodynamics. The Astrophysical Journal, 567:81–83, 2003. https://doi.org/10.1086/339850
D.A. Shalybkov and V.A. Urpin. The Hall effect and the decay of magnetic fields. Astronomy & Astrophysics, 321(2):685–690, 1997.
R. Wan and Y. Zhou. On global existence, energy decay and blow-up criteria for the Hall-MHD system. Journal of Differential Equations, 259(11):5982–6008, 2015. https://doi.org/10.1016/j.jde.2015.07.013
R. Wan and Y. Zhou. Global well-posedness, BKM blow-up criteria and zero h limit for the 3D incompressible Hall-MHD equations. Journal of Differential Equations, 267(6):3724–3747, 2019. https://doi.org/10.1016/j.jde.2019.04.020
R. Wan and Y. Zhou. Global well-posedness for the 3D incompressible Hall-magnetohydrodynamic equations with Fujita-Kato type initial data. Journal of Mathematical Fluid Mechanics, 21(5):1–18, 2019. https://doi.org/10.1007/s00021-019-0410-0
M. Wardle. Star formation and the Hall effect. Astrophysics & Space Science, 292:317–323, 2004. https://doi.org/10.1023/B:ASTR.0000045033.80068.1f
S. Weng. On analyticity and temporal decay rates of solutions to the viscous resistive Hall-MHD system. Journal of Differential Equations, 260(8):6504–6524, 2016. https://doi.org/10.1016/j.jde.2016.01.003
X. Wu, Y. Yu and Y. Tang. Well-posedness for the incompressible Hall-MHD equations in low regularity spaces. Mediterranean Journal of Mathematics, 15(2):1–14, 2018. https://doi.org/10.1007/s00009-018-1096-x
X. Zhao. Decay of solutions to a new Hall-MHD system in R3. C. R. Math. Acad. Sci. Paris, 355(3):310–317, 2017. https://doi.org/10.1016/j.crma.2017.01.019
